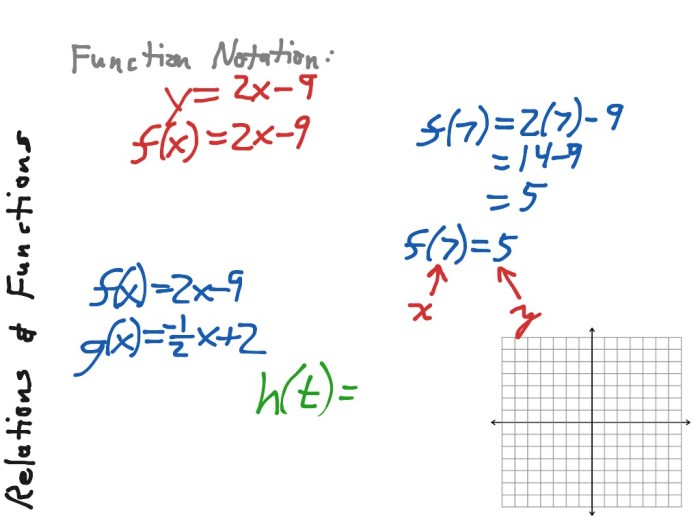Delving into the realm of Unit 2 Linear Functions Answer Key, we embark on an intellectual journey that unravels the intricacies of linear functions, empowering us with the knowledge to solve equations, graph functions, and decipher real-world applications.
As we navigate this mathematical landscape, we will explore the defining characteristics of linear functions, their equations, and their graphical representations. We will delve into techniques for solving linear equations, avoiding common pitfalls, and harnessing the power of graphing tools to visualize these functions.
Unit 2: Linear Functions: Unit 2 Linear Functions Answer Key
Linear functions are fundamental concepts in algebra that represent linear relationships between two variables. They are widely used in various fields to model and solve problems.
Key Concept Review: Linear Functions
A linear function is an equation that describes a straight line. It is expressed in the form y = mx + b, where m is the slope and b is the y-intercept.
The slope represents the rate of change of the dependent variable (y) with respect to the independent variable (x). A positive slope indicates an upward trend, while a negative slope indicates a downward trend.
The y-intercept represents the value of the dependent variable when the independent variable is zero.
Solving Linear Equations
Solving linear equations involves finding the value of the variable that makes the equation true. There are various methods for solving linear equations, including:
- Substitution: Substituting the value of one variable into the equation and solving for the other variable.
- Elimination: Adding or subtracting the same quantity from both sides of the equation to eliminate one variable.
- Graphical: Graphing the equation and finding the x-intercept, which is the solution to the equation.
Graphing Linear Functions
Graphing linear functions involves plotting points and drawing a line that represents the equation. The steps for graphing a linear function include:
- Plotting the y-intercept on the y-axis.
- Using the slope to find additional points.
- Connecting the points to draw a line.
Applications of Linear Functions, Unit 2 linear functions answer key
Linear functions have numerous applications in real-world scenarios. They are used to model various phenomena, such as:
- Distance traveled as a function of time (e.g., in physics)
- Cost as a function of quantity (e.g., in economics)
- Temperature changes as a function of altitude (e.g., in meteorology)
Question Bank
What is the equation of a linear function?
y = mx + b, where m is the slope and b is the y-intercept.
How do you solve a linear equation?
By isolating the variable on one side of the equation.
What is the slope of a line?
The ratio of the change in y to the change in x.